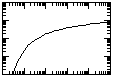
here plotted as log(W(u)) vs. log(1/u)
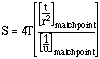
| The ground-water flow equation for radial flow to a well in a confined aquifer | |
| Drawdown (s(r,t)) as a function of distance (r) from the well and time (t) since the initiation of pumping--the Theis solution for the case of a fully-penetrating well pumping at a constant rate from a non-leaky, isotropic and homogeneous confined aquifer of infinite extent | |
| The "u" parameter for the "Well Function," W(u), for the Theis solution. | |
| The Well Function, which can be calculated by the series expansion shown below. | |
 |
here plotted as log(W(u)) vs. log(1/u) |
| If drawdown in one or more observsation wells is measured in response to pumping (example), then we can inversely find the Storativity (S) and Transmissivity (T) of the aquifer. | |
| Theis log-log type-curve matching method | |
 |
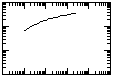
Plot log(s(r,t)) vs. log(t/r2) (observed drawdown data (example)) to the same scale as a plot of the Well Function (log(W(u)) vs. log(1/u)), match the curves and find the corresponding coordinates of an appropriate "match point." |
| Transmissivity can be determined from the W(u) and s(r,t) coordinates of the matchpoint. Transmissivity has units of units of length2/time, e.g. m2/sec. | |
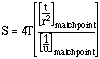 |
Storativity can be determined from the 1/u and t/r2 coordinates of the matchpoint. Storativity is dimensionless. |
| Jacob-Cooper semi-log Time-Drawdown method | |
| If the pumping time (t) is long enough (or r is small enough)
then the "u" parameter becomes small enough ( | |
 |
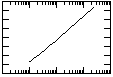
Plot s(r,t) (linear scale) vs log(t) (observed drawdown data (example)), and find the slope of the line. |
| Transmissivity can be found from Ds = s(t2)-s(t1), when Dt is chosen such that t2 = 10xt1 as therefore log (t2/t1) = 1 | |
| Solve for Storativity using any values of s(t) and t, for example s(t)=0 when t=t0. | |
| This is a necessary check of validity, to meet the assumptions inherent in the semi-log analysis. | |
| Theim method for steady-state flow (distance-drawdown) | |
| If |
|
| the Theim equation can be solved for Transmissivity. Storativity cannot be determined, as there is no transient behavior (no change in storage). Note that this result has the same form as would the Jacob-Cooper Distance-Drawdown semi-log method. | |
| Keep these assumptions in mind! | |
| We are assuming a fully-penetrating well pumping at a constant rate from a non-leaky, isotropic and homogeneous confined aquifer of infinite extent. For the Jacob-Cooper method we are further assuming that t is large enough that the plot of s(t) vs. log(t) is a straight line. For the Theim method, we are assuming a steady-state has been reached. | |
| Note that since the Theis solution is linear, it is possible to use superposition and "image wells" to deal with changes in pumping rate and aquifer boundaries. | |